[7일차] 경사하강법
경사하강법,,아 ㅇㄱㅇ 교수님 너무 그립고 정말 감사하고 아직까지도 그 때 필기 겁나 찾아봅니다,,강의력짱짱맨
분명 이해는 가는데 중간중간 생략이 너무 많아서 멘붕도 같이 오는 날이었다.
그럼 정리하며 하나하나 기억해보자.
미분
미분 하는 법 등등은 생략하고,
파이썬의 많은 라이브러리들이 미분을 지원한다. 아래 코드를 보자

👆위에처럼 미분 결과를 보여준다!
경사하강법/경사상승법
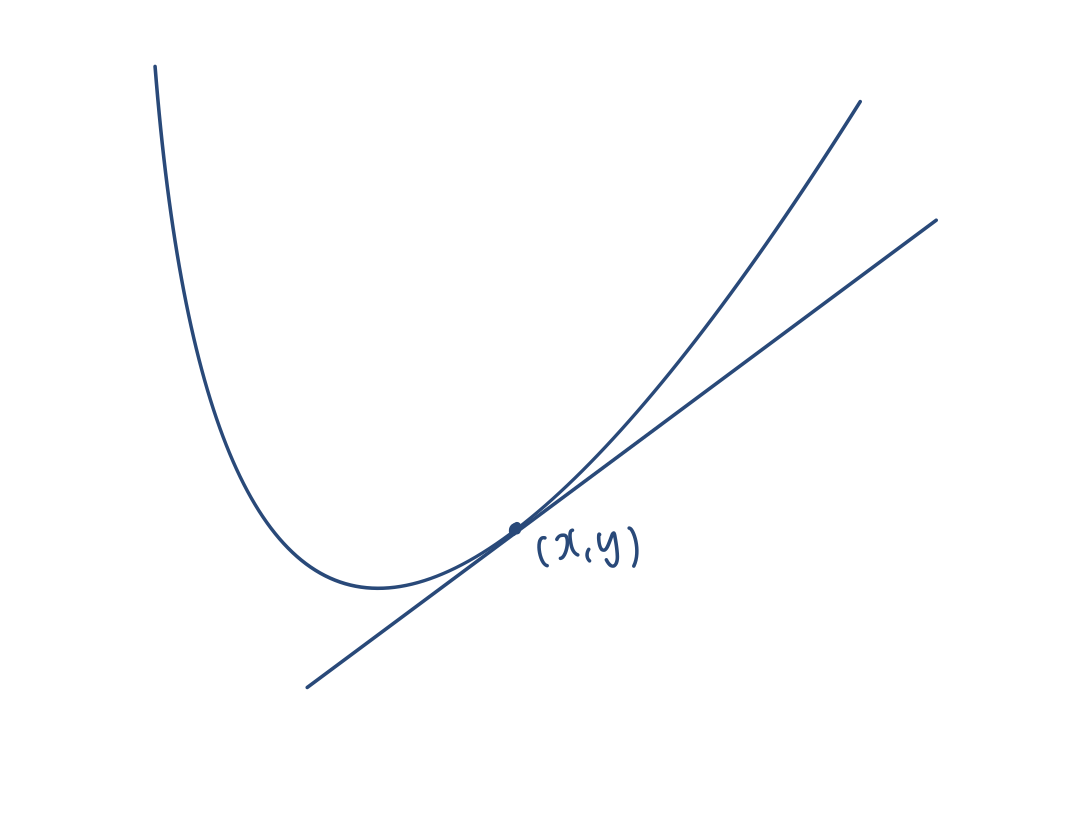
👆우리의 목표는 저기 저 볼록한 부분의 좌표를 아는거라고치자,
점 (x,y)에서의 기울기를 알면 어느 방향으로 점을 이동시켜야 볼록한 부분으로 갈 수 있는지 알 수 있다.
즉 미분값을 알면 점의 이동 방향을 알 수 있다.
여기선 미분값이 양수일테니, 어떠한 수를 빼주면 볼록한 부분으로 이동할 수 있다.
만일 더한다면 최대값을 찾아 떠날 수 있겠지?
이렇게
미분값을 더하면 함수를 최대화 할 수 있고 : 경사상승법(gradient ascent)
미분값을 빼면 함수를 최소화 할 수 있다! : 경사하강법(gradient descent)
그림과 함께 정리하자면

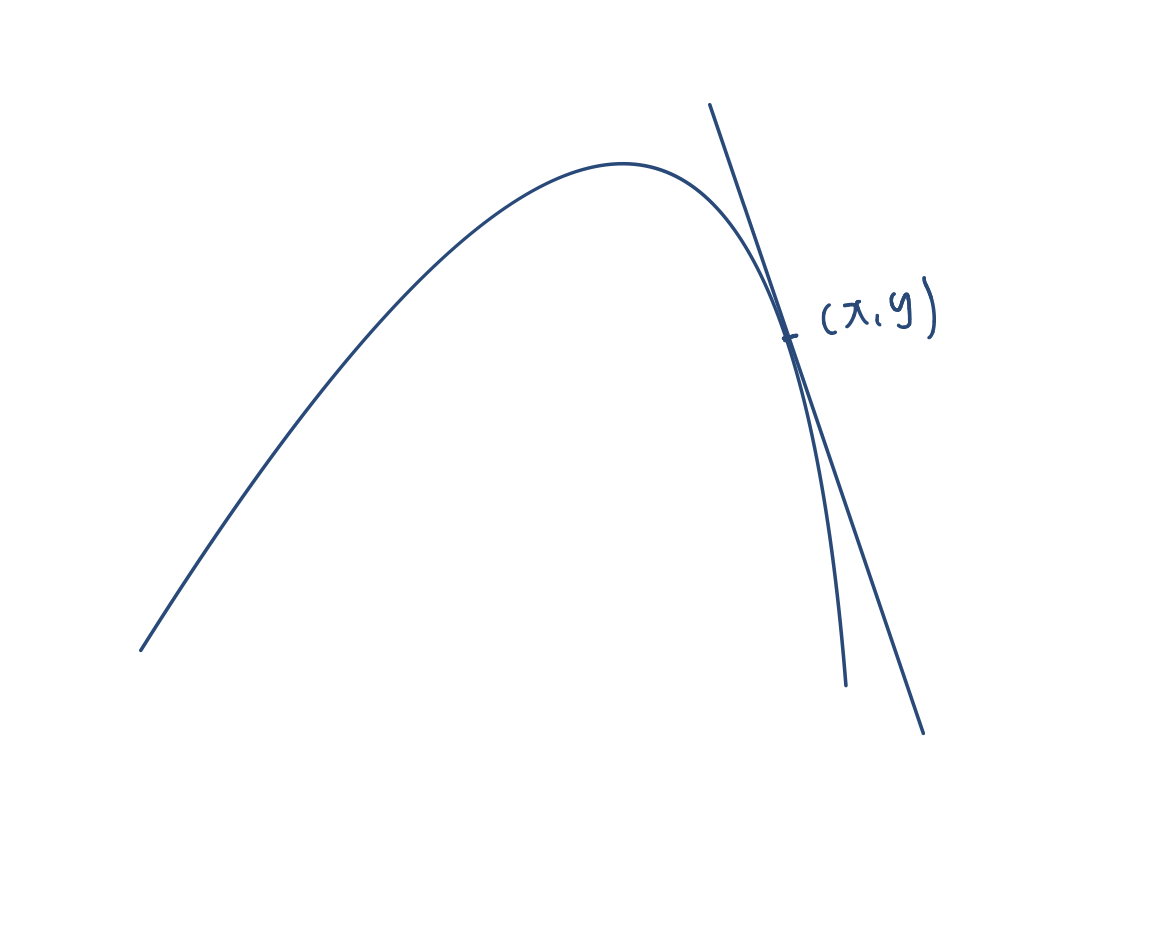
👆미분값이 양수다 -> 더하면 최대값을 찾아 간다(위로 퍼지는 부분) 👆 미분값이 음수다 -> 더하면 최대값을 찾아 간다(볼록한 부분)
-> 빼면 최소값을 찾아 간다(오목한 부분) -> 빼면 최소값을 찾아 간다(밑으로 퍼지는 부분)
이렇게 간단하다구~.~
경사하강법 알고리즘
알고리즘으로 표현하면 어떤지 살펴보자
var = init
grad = gradient(var)
while(abs(grad) > eps):
var = var -lr * grad
grad = gradient(var)각 줄 별로 살펴보자
- init은 시작점이다. 위의 예시에서 (x,y) 처럼 임의의 점이다
- gradient는 미분을 계산하는 함수이다. 점을 넣어서 미분을 계산한다.
- 우리의 목표는 볼록 혹은 오목한 곳을 찾는 것이기 때문에 미분값이 0이 되는 시점을 찾는 것이다. 단 컴퓨터로 미분값이 정확이 0이 되는 점을 찾는 것은 불가능하므로 eps라는 종료조건을 넣어준다. 해당 값보다 작아질 때 까지 반복한다.
- 이건 경사하강법이기 때문에 미분값을 빼준다. lr은 임의의 상수인데, 점을 어느 정도 이동시킬지 보폭을 정하는 상수이다. 학습률이라고 부르며 미분을 통해 업데이트 하는 속도를 조절해야한다!
- 조건에 다다를 때 까지 반복적으로 미분값을 업데이트한다.
이러면 완벽히 이해가 될 것이다 하하
실제 코드는 아래와 같다.

👆함수 하나 하나 살펴볼까?
우리는 x^2 + 2x+3의 최소점을 구하려고한다. 정답은 알고 있다 (-1,2) 일 때 최소값이다!

gradient 함수는 해당 식의 미분값을 계산해준다. 즉 var*2+2 를 반환한다!
gradient_descent는 위에서 설명한 바와 똑같이 돌아간다.
아주 간단~
나온 값이 미분값이 0이 되는 (-1,2)라는걸 확인하는건 어렵지 않다~
변수가 여러개일때는?
그러니까 이런경우다

이런 경우엔 어떻게 해아할까~~ 당근 편미분을 하면 된다~~
각 변수별로 편미분을 계산한 gradient 벡터를 이용하면 된다!
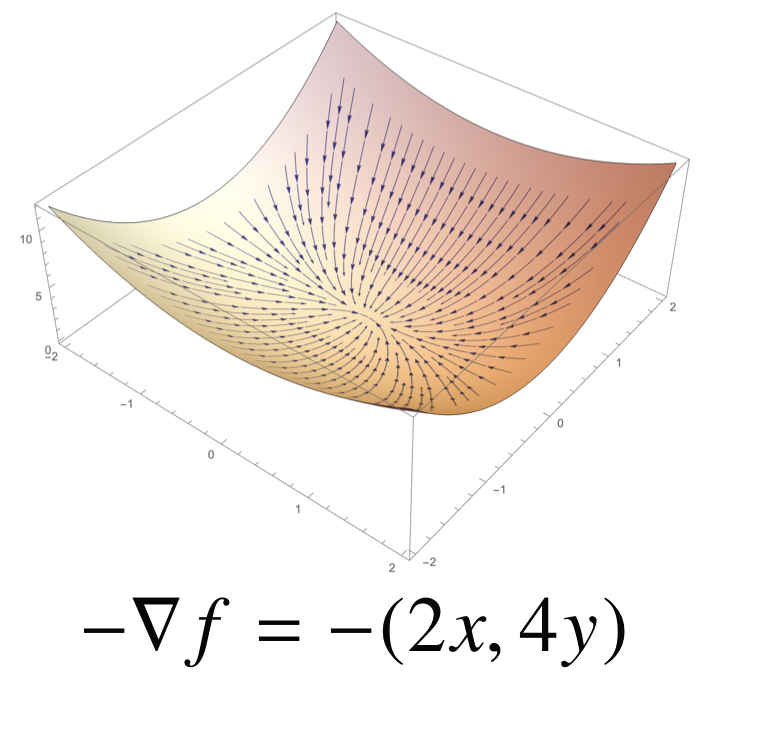
그러면 이런 아리따운 방향성이 생긴다~
경사하강법 알고리즘 again
var = init
grad = gradient(var)
while(norm(grad) > eps):
var = var -lr * grad
grad = gradient(var)위의 알고리즘을 그대로 쓰되 abs를 norm으로만 바꿔주면 된다.
여기서 좀 헷갈리는게ㅋㅋㅋㅋnorm이 좀 갑자기 튀어나왔다
여기서 norm은 우리가 여태 배운 l2 norm을 뜻하는건 아니고 관용적으로 RMSE를 l2norm 처럼 쓴다고 한다!
그러니까 오류값을 최소화하는 하는 점을 찾겠다는거다!

이건 regression 모델에서 error를 측정하는 방법들인데 RMSE가 l2 norm이랑 똑같이 생기긴했네!
여기까지 경사하강법의 순한맛이었다~ 하하 아직 매운맛은 시작도 안했지 ㅎㅎㅎ
선형회귀분석에 경사하강법을 적용시키자
이제 선형회귀분석으로 다시 돌아온다.
선형회귀분석의 목적은 데이터(점)들을 가장 잘 나타내는 선 하나를 찾는거다.
유사역행렬을 이용하는 방법도 있지만, 경사하강법을 이용하는 방법도 있다!
우리는 데이터를 잘 나타내는 선 하나를 찾는거고 그렇기에 목적식이 y-ax <--이다
뭐 y 절편은 뺏다고 치고, 모든 데이터를 y-ax에 넣었을 때 0이 된다면 그게 바로 데이터를 잘 설명하는 선이다.
하지만 그건 불가능하니 error rate가 최소인 y-ax식 즉 a을 찾아야한다. 여기서도 error rate는 RMSE 즉 L2norm을 기준으로 한다.
그럼 gradient vector를 구해야겠지?

뭐 이런 식을 거쳐서 벡터가 나온다.
그럼 저 벡터를 이용해서 최소화하는 식을 구하면

뭐 이런 식이 나온다 뚝딱뚝딱
자세한 내용은 내일 피어세션 이후에 추가할 예정~
그럼 이제 이 식을 가지고 알고리즘을 만들어보자
경사하강법 기반 선형회귀 알고리즘
for t in range(T):
error = y - X @ a
grad = -transpose(X) @ error
a -= lr * grad- 이번엔 while이 아니라 t다 학습 횟수를 정해준다
- error라 함은 y - X @ a의 값은 원래 0이 되어야 하는데 그렇지 못하니까 그 값을 error로 친다
- 공식에 맞춰서 grad를 구해준다, 어느방향으로 얼만큼 움직일지 결정해주는 역할을 한다
- lr은 학습률이고, 그에 맞춰 a의 값을 변경해준다.
기존 경사하강법과 동일하니 겁먹을 필요 없다.
확률적 경사하강법
경사하강법은 미분가능하고 볼록한 함수에 대해서만 사용가능하다. 당연하다 미분값이 가장 작아지는 값을 찾는건데 미분이 안되면 말도 안되는거고, 볼록한 함수 즉 경사 "하강"을 하면서 찾을 수 있는건 최솟값이다. 즉 볼록한 함수에서만 사용가능한거다.
근데 만약 그래프 모양이

요따구라면 초기점에 따라서 local한 최소값을 찾게된다..! 그럼 global한 최소값과 차이가 있을 수도 있다는거지
이를 보안한게 확률적 경사하강법이다 (stochastic gradient descent) 편의상 SGD라고 부르겠다.
모든 데이터를 이용하는게 아니라 하나 혹은 일부 데이터(미니배치)만을 이용하여 값을 결정하는거다!
딥러닝의 경우 SGD가 경사하강법보다 실증적으로 더 낫다고 검증되었기에 안심하고 쓰자
데이터 중 일부만 쓰기 때문에 그 비율만큼 연산량이 감소한다.
미니배치를 확률적으로 선택하기 때문에 목적식이 계속 바뀐다! 데이터가 확률적으로 변하니까, 그 데이터를 표현하는 선도 계속 변하는건 당연한거다.
global한 답을 찾을 수 있는건, 목적식이 계속 변하기 때문에 local한 답에서 벗어날 가능성이 주어지기 때문이다!

성능이 훨씬 좋은 것도 확인할 수 있다(물론 미니배치의 수가 너무 작으면 성능이 더 안좋을 수도 있으니 미니 배치에 신경쓰자)
데이터를 쪼개서 계산하기 때문에 병렬적으로 처리가 가능하다 아주 귯
오늘은 여기까지이다. 공식 추출부분만 빼면 개념적으론 수월했던 하루였다. 내일도 화이팅하자!