[11일차] DL Basic / 베이즈 통계학 햘짝

DL Basic먼저 정리할거다. 왜냐면 하고싶으니까ㅎㅎ

 

아니 이렇게 못끝낸 티스토리 11일만인데 오늘따라 구글시트 통해서 들어온 사람이 몇 잇네......저 원래 진짜 맨날 햇어요....어제만 일이 있었다고 집안일...흑흑....... 하튼 아직도 작성중....

 

먼저, 역사적인 흐름을 쭉 훑어주셨는데 너무 좋았다. 전체 적인 흐름을 잡고 공부하면 더 잘된다.

이 흐름 이후에 가장 간단한 MLP의 구현까지 나갔다.

 

딥러닝의 key components는 네가지가 있다.

• data
• model
• loss function
• algorithm

자세한 설명은 생략해도 좋을 듯 하고..

AI의 역사에서 큰 역할을 한 모델들을 쭉 나열해주셨다. 

하나하나 배워갈 때 마다 이 게시글에 와서 밑줄 쫙 그을거다.

 

2012년 AlexNet

처음으로 딥러닝이 대회에서 우승먹기 시작한 모델이라고 한다. 이후로는 DL이 우승을 내준적이 없다고 한다. 그만큼 DL의 판도를 바꾼 모델이다. 이미지를 분류하는건데 convolution network 모델이다.

2013년 DQN

그 유명한 알파고를 만든 deep mind에서의 강화학습 모델이다

구글에 M&A하는 해피엔딩!

 

2014년 Encoder/Decoder

NLT 즉 번역기이다. 구글 번역기도 이 모델을 쓴다고 한다.

 

2014년 Adam Optimizer

가장 많이 쓴다고 한다. 그냥 이유도 없이 쓴단다.

그만큼 성능이 잘 나온단다. 사실 반쯤 이해못했다 다음에 설명하실 때 다시 이 문단을 채우러 돌아오겠다.

 

2015년 GAN

난 ....GAN이 너무 제대로 배우고 써먹고싶었다. 언능 배우고싶다!!!!!!!

나도 논문에 영감을 준 술집 이름을 쓰는 멋진 사람이 되어야지

 

2015년 Residual Networks

기존에는 network가 너무 깊으면 training에만 잘 맞고 test에서는 잘 맞지 않아서 깊게 만들지 못했다고한다(오버피팅 말하는건가?)

하지만 이 연구 덕분에 딥한 런닝이 가능해졌다고 한다.

 

2017년 Transformer

Attention is all you need

어떻게 논문 제목을 저렇게 짓지? 아무것도 모르는 내가 봐도 대단하다. 근데 가오잡은게 아니라 찐이었댄다.

 

2018년 BERT (fine-tuned NLP models)

다양한 단어와 뭉치들을 이용해 미리 모델을 만들어 놓고 원하는 data에 맞춰서 fine하게 튜닝하는 모델이라고 한다.

 

2019년 BIG Languate Models

BERT의 끝판왕이라고 한다. 양간의 fine tuning을 통해 다양한 문장/프로그램/표 등 sequetial한 모델을 만들게 해준다고 한다.

파라미터가 무지막지하게 많아서 (175billion) BIG이라고 이름지었댄다. 역시 단순하다.

 

2020년 self supervised learning

2020년....이게 참 무섭다 아주 열렬히 성장중인 업계라는 증명이쟈나 내가 이 분야에서 잘 해낼 수 있을까

학습 data외에도 label을 모르는 unsupervised data를 활용한다는 모델이다. 대단하다.

 

-------------------------------------------------------------------------------------------------------------------

MLP

Neural Networks

뉴럴 네트워크는

Neural networks are function approximators that stack affine transformations followed by nonlinear transformations.

function approximators란 파라미터를 이용하여 실제값에 근접하는 함수이다.

이 근사하는 함수는 affine변환과 nonlinear 변환의 누적이다.

 

Linear Neural Networks

뉴럴 네트워크 중에 가장 간단한 형태이다.

모델이 y=wx+b 형태니까.

loss function은 MSE이다

 

loss를 미분하여 얻은 값과 stepsize를 이용해 w와 b값을 조정한다.

 

w가 하나의 상수일 필요는 없다. multi dimesional input이 들어오면 그에 맞는 w행렬과 b벡터를 내보내면 된다.

w행렬에 대한 이야기는 raiknow.tistory.com/77 를 참고!

 

위의 게시글에는 w 행렬의 dimension에 대한 내용만 담고 있고, 그 다음 layer에 대해서는 살포시 생략했었다.

여기선 그걸 살펴보자면,

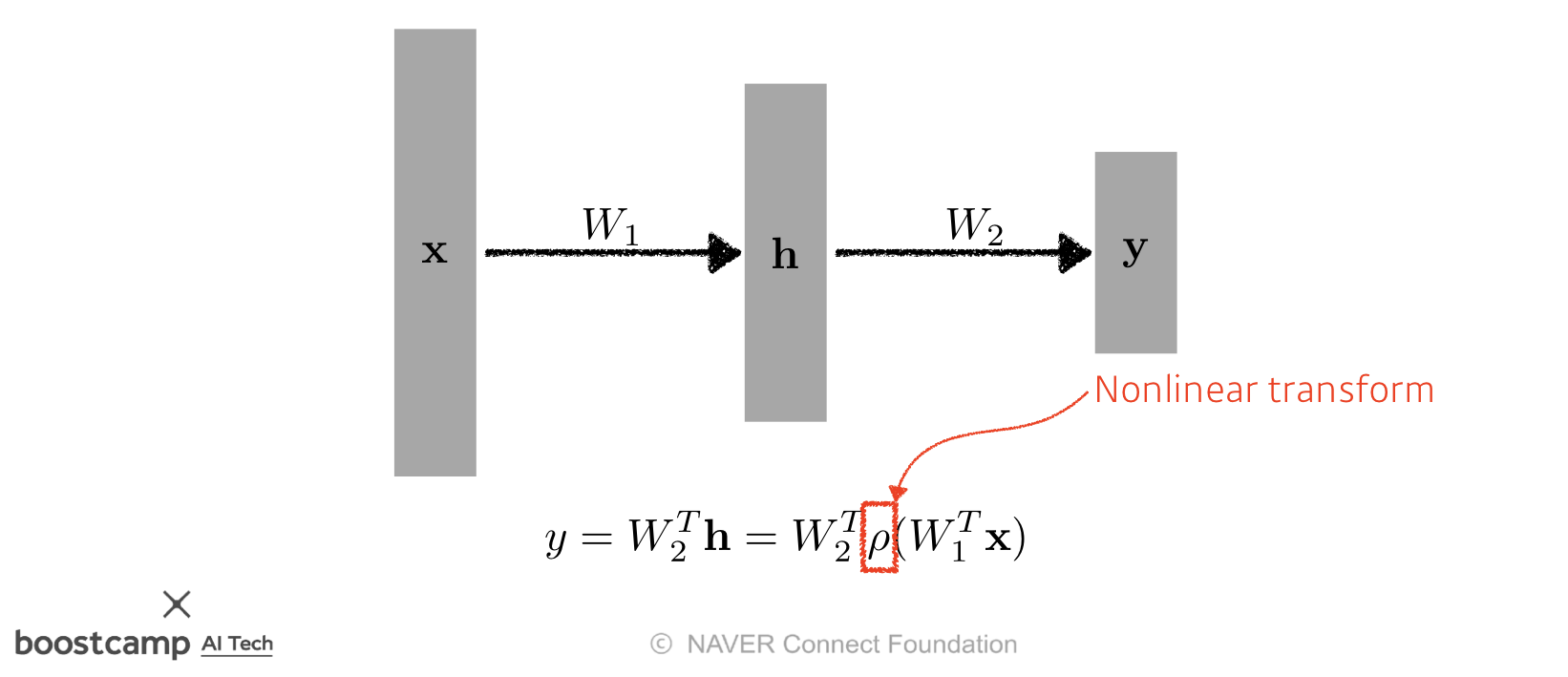
👆가운데 hiddenlayer를 거치고 나면 거기서 나온 값으로 또 무언가를 한다. 결국 위의 그림이 하나의 layer가 된다.

마지막으로 해주는건 마로 activation function을 거치는거다. 이전 수업에서 정리한적 있는 그거 맞다. linear를 nonlinear로 바꿔주는 ReLU sigmoid 등등의 함수들이다. 

 

hidden layer가 하나 있는 NN은 대부분의 연속적인 함수에 근사할 수 있다는 논문이 있다고 한다.

그런걸 찾을 수 있다는 것 보단 단순히 존재성만 보장하고 있다!

 

이렇게 w들을 lossfunction으로 열심히 수정해가며 계속 업데이트 한다~(앞에서 정리했던 내용이라 생략)

 

-------------------------------------------------------------------------------------------------------------------

베이즈 통계학

 

베이즈 통계학은 classification을 위한 방법 중 하나이다.

심플하게 말하자면 P(E | H)를 통해 P(H | E)를 얻는 방법이다.

예를 들어보자.

 

어떤 사람이 여드름이 너무 심해져서 병원에 왔다.

 

여드름이 심한 사람이 청소년기일 확률을 구하는 것 보다,

청소년기인 사람 중 여드름이 있는 사람을 구하는게 더 쉽다는 뜻이다.

 

식으로 정리해보자면 

 

 

👆위와 같다.

조건부 확률 공식으로 요리조리 가지고 놀다보면 저런 식이 나온다.

 

그러니까, 여드름이 심한 사람이 청소년기일 확률을 구하기위해

여드름이 심한사람, 청소년기인사람, 청소년기인 사람 중에 여드름이 심한 사람의 확률을 구하는게 더 쉽다는 논리이다.

 

이런식으로 사후확률을 구해보자.

 

강의에 나온 예시의 숫자를 그대로 쓰기 위해 비율이 좀 이상할 것이다. 하하

 

어떤 나라가 있다. 고령화 문제가 아주 심각한 나라이다.

이 나라에서 청소년의 비율은 10프로이다.

주민등록 체계가 아주 살짝 잘못되어서 실제 청소년이 청소년이라고 확인될 확률은 100프로가 아닌 99프로이다.

청소년이 아닌데 청소년이라고 확인될 확률은 1프로이다.

 

이 때 청소년이라고 확인 되었는데 실제로 청소년일 확률은 얼마나 될까?

이건 아주 중요한 문제이다. 술집에서 청소년에게 술을 팔다가 걸리면 아주 큰일이 나기때문에 사람을 확인해보았는데, 청소년이란다! 근데 그 사람은 억울하대! 자기가 진짜 청소년이 아니라고 박박 우기고 있다. 자기 나라 주민등록 체계가 이상해서 그런거란다. 술집 주인은 아주 난감할거다.

 

👆결론부터 이야기 하자면 그 사람은 91프로의 확률로 청소년이다. 술집 주인은 어쩔 수 없이 그 사람을 내쫓을 것이다.

(공식에 숫자들을 넣기만 하면 되니까 자세한 설명은 생략한다)

 

이 나라가 이런식으로 굴러가다가 망해서 민심이 안좋아져서 정권이 바뀌었다.

아 그런데 아쉽게도 이번 정권도 제대로 일을 해내지 못했다. 심지어 조금 더 심해졌는데

청소년이 아닌데 청소년이라고 확인될 확률이 10프로로 늘어버렸다.

 

이런.. 식당 주인은 난감하다. (어쩌다보니 번역투가 됐네ㅋㅋㅋㅋㅋㅋ)

그래서 이 사람이 정말 청소년일 확률을 다시 구해봤다.

👆아니 결과가 기가 막힌다.

고작 1프로에서 10프로가 된건데 이 사람이 청소년일 확률이 52프로 밖에 안된다. 식당 주인은 돈을 벌어야 하기 때문에 그냥 오검이라고 믿어버리고 술을 팔아버린다..

 

식당 주인은 아무래도 찜찜해서 그 사람이 술마시며 하는 대화를 훔쳐듣고있는데 야자 얘기 나오고~ 담임 얘기 나오고~ 아무리 봐도 고딩같은거다. 이미 영업정지의 경험이 있던 주인은 다시 검사하자며 손님을 다시 검사한다. 근데 또 청소년이라고 나와버렸다.

 

우리는 앞서 계산한 사후확률(0.524)를 이용하여 갱신된 사후 확률을 계산할 수 있다. 

 계산된 사후확률이 다음 계산 때는 사전 확률로 쓰인다.

 

 

그러니까 위 그림의 사전확률은 0.524, 가능도는 바뀌는게 아니니까 원래 주어진 0.99

P(D)만 구하면 갱신된 사후 확률을 구할 수 있다.

이전에 참일 확률이 0.524이고 거짓일 확률이 0.476이었다.

그래서

P(D)= (청소년이라고 결과가 나왔는데 정말 청소년일 확률) * (그게 참일 확률) + (청소년이라고 결과가 나왔는데 잘못나올 확률) * (그게 거짓일 확률)

      = 0.99 * 0.523 + 0.1 * 0.476 = 0.566

이란 결과가 나온다

 

결과적으로 0.524 * 0.99 / 0.566 = 0.917 확률이 나온다.

 

식당주인은 극대노하여 91퍼센트 확률로 청소년일 사람을 내쫓았다.

~해피엔딩~

 

조건부 확률로 할 수 있는건 이 뿐만이 아니다.

👆이렇게 다양하게 정밀도 민감도 등을 추출할 수 있다.

보통 산업에 따라 FP와 FN 중 중요한 걸 줄이는 방향으로 간다.

어후 이건 진짜 매번 볼 때 마다 헷갈려~!~!

 

여기서 조건부 확률을 오해하면 안된다는 말을 하며 마무리 지으려 한다.

조건부 확률을 인과관계로 해석해서는 안된다. 절대.

실제 원인이라면 조건부 확률을 이용하여 여러가지 통계를 낼 수 있겠지만

 

조건부 확률 자체가 인과관계를 보여주진 않는다.

 

👆심지어 위와 같은 역설적인 상황가지 나올 수 있기 때문에 조정효과를 통해 Z의 개입을 제거해야한다.

 

 

드디어 끝~