[21일차] 그래프 시이작

boostcamp AITech

[21일차] 그래프 시이작

라이크나우 2021. 2. 22. 23:23

벌써 21일...ㅇㅁㅇ

오늘은 간단했따 아주 좋다

(뒤에 코드부분은 아직 작성을 못했다)

한페이지로 정리해보았는데...다 담겼을지 한번 봐보자.

그림에 담긴건 📝, 안담긴건 ❎표시를 할거다 왜냐면 내맴

📝Graph는 Network라고도 부르며

정점(vertex)

노드(node)

간선(edge, link)로 이루어진 수학적 구조이다.

❎그래프는 복잡계(complex system)의 구성 요소 간의 상호작용을 표현한거다.

❎친구관계, 전자 상거래 구매 내역, 정보통신 혹은 Web, 뇌의 뉴런 연결, 지식 그래프, 화학 분자, 단백질 상호작용, 세포간 유사도 그래포, 이미지 분해 등에 쓰인다.

📝A 그래프와 D그래프는 간선의 방향 유무를 나타낸다.

A그래프는 협업 관계 혹은 페이스북 친구 그래프 등을 표현할 수 있고

D그래프는 논문 인용 그래프, 트위터 팔로우 그래프를 표현할 수 있다.

📝A그래프와 C그래프는 가중치의 유무를 나타낸다.

C그래프는 전화 그래프(전화를 몇번 주고받았는지, 유사도 그래프 등을 표현할 수 있다.

📝A그래프와 B그래프는 동종 그래프인가/ 이종 그래프인가에서 차이가 난다.

이종 그래프는 다른 종류의 정점 사이에서만 간선이 연결된다. 전자 상거래 구매내역 혹은 영화출연 그래프 등이다.

📝A그래프를 집합으로 나타내면 그림과 같다. 이웃들을 표시하면 된다.

📝D그래프 역시 그림처럼 in out 을 구별해서 적어주면 된다.

📝그래프 상의 경로, 거리 및 지름

경로 : u에서 v까지 정점들의 순열
- u에서 시작해서 v로 끝나고
- 다 연결되어있어야함
- 중복이나 뭐 그런건 상관 없다.
- 경로의 길이는 간선의 수 즉 node-1이다
거리 : 경로 중에 최단 경로의 길이
지름 : 정점 간 거리의 최댓값

📝연결성

해당 정점과 연결된 간선의 수

위의 그림과 같이 d()로 표현한다.

📝연결 요소

연결 요소에 속하는 정점들은 경로로 연결될 수 있다.

위의 조건을 만족하면서 정점을 추가할 수 없다.

복잡하게 적혀있지만 결국 덩어리들을 의미한다. 위의 그림에서는 A, B, C, D가 각각의 연결 요소이기 때문에 4개가 존재한다고 보면 된다.

❎해결할 수 있는 문제의 예시

정점 분류(node classification) 문제 : 정점이 여러 유형을 가진 경우 각 유형을 추측한다.

ex)

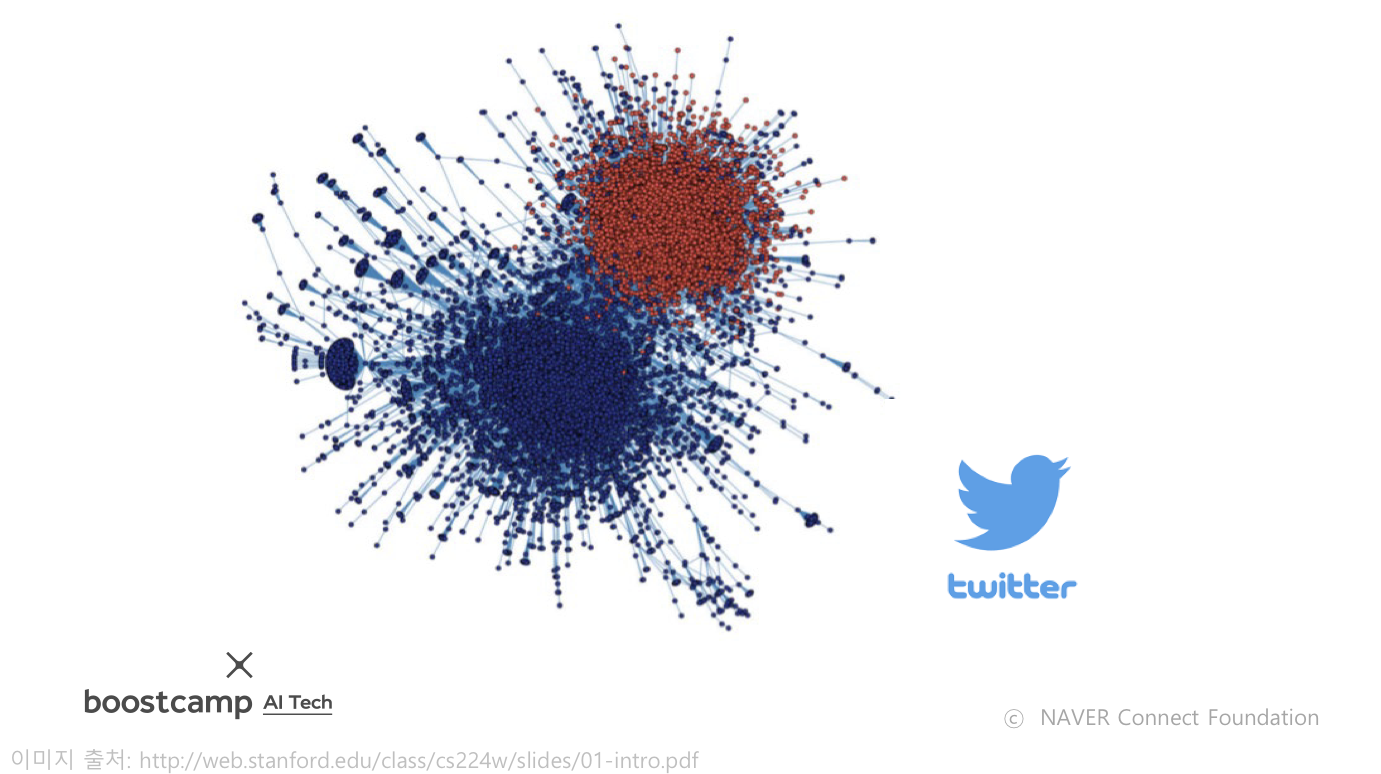
트위터에서의 공유 관계(리트윗)를 분석하여, 각 사용자의 성향을 예측

연결 예측(Link Prediction) 문제 : 거시적인 관점에서는 주어진 그래프가 어덯게 성장할지 예측하는 방향으로 쓰인다

미시적인 관점에서는 각 정점이 앞으로 어떤 정점과 연결될지 예측할 수 있다. 추천시스템에 쓰인다.

ex)

어떤 물건을 구매해야 만족도가 높을지 예측(어떤 물건 즉 어떤 노드와 연결되어야 만족도가 높을지 예측)

군집분석(community detection) 문제 : 밀접하게 연결된 정점들의 집합 즉 군집을 찾는다. 연결 관계로부터 사회적 무리 등을 찾는데 쓰일 수 있다.

랭킹(ranking), 정보 검색(information retrieval) 문제 : 웹이라는 거대한 그래프로부터 중요한 웹페이지 찾기 등

정보 전파(information cascading) 및 바이럴 마케팅(viral marketing)문제 : 정보가 네트워크 속에서 어떻게 전달되는지

import networkx as nx                           # NetworkX
import numpy as np                              # 선형대수를 위한 라이브러리
import matplotlib.pyplot as plt  

#그래프를 초기화 한다. Graph()는 방향성이 없고, DiGraph는 방향성이 있다.
G= nx.Graph()                                 
DiGraph = nx.DiGraph()                        

#node 즉 정점을 추가해준다.                                      
G.add_node(1)          
#넘버 오브 노드스,,말 그대로 정점의 수를 반환해준다. 이 경우는 1개겠지
print(str(G.number_of_nodes())    
# node의 목록을 리스트형태로 전부 반환한다.
print(str(G.nodes))                  

#정점 1 ~ 10을 추가해준다.
for i in range (1, 11):
    G.add_node(i)
    
#아래는 edge 즉 간선을 추가하는 코드이다. 우선 초기화시켜준 다음에 노드 두개를 파라미터로 넣어주면 둘 사이에 연결관계가 생긴다.           
G = nx.Graph()                                 
G.add_edge(1, 2)         
print(str(G.nodes)) # node의 목록 반환 #[1, 2]
print(str(G.edges)) # edge의 목록 반환 #[(1, 2)]

설명은 안에 주석으로 달았다. 간단하니 간단히 설명하고 넘어가즈아

print("#Add edge (1, i) for i = 2 ~ 10")                   
for i in range (2, 11):
    G.add_edge(1, i)
print("Graph : " + str(G.edges) + "\n")


#node의 위치를 대충 정하면 단순한 그래프도 괜히 복잡해 보일 수 있다 그래서 spring_layout으로 점 위치를 지정해준다.
pos = nx.spring_layout(G)  

# 정점의 색과 크기를 지정
nx.draw_networkx_nodes(G, pos, node_color="red", node_size=100)    

# 간선도 표현
nx.draw_networkx_edges(G, pos)                       

# 각 정점의 라벨도 표현
nx.draw_networkx_labels(G, pos, font_size=10, font_color="black")       
plt.show()

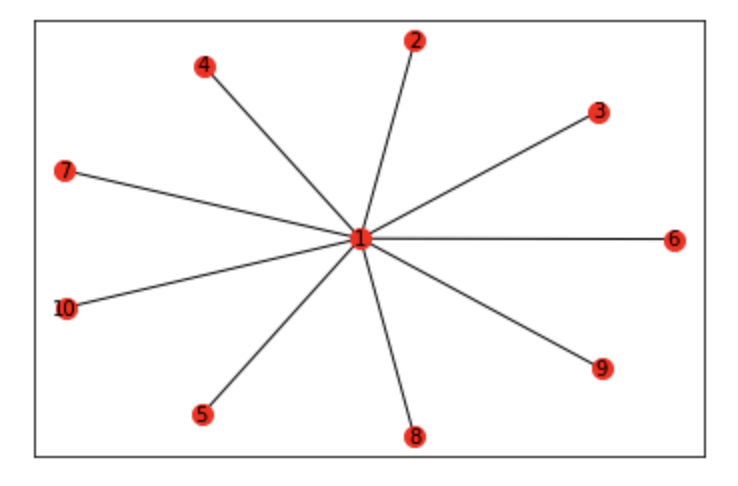
먼저 위치를 지정해주고,

해당 위치 출력될 node 색깔과 사이즈를 결정,

간선도 출력,

라벨도 사이즈와 색을 정해서

시각화 할 수 있다!

랜덤그래프

뭐 실제그래프는 ㄹㅇ 현실에 있는 실제 그래프고

랜덤 그래프는 만들 수 있는 여러가지 방법이 있겠지만, 기본적으로 확률적 과정을 통해 생성한 그래프를 의미한다.

오늘 배운건 에르되스-레니 랜덤 그래프인데

G(n,p) 라 함은 n개의 node를 가지고, 두 개의 node 사이에 edge가 존재할 확률이 P라는 것이다.

단 정점 간의 연결은 항상 독립적이다!

위의 예시를 보면 이해가 빠를거다.

작은 세상 효과

예전에 싸이월드 시절에 몇다리만 건너면 일촌이다 뭐 이런 말이 한창 돌아서 나도 막 파도타기인가 이웃타기인가 하면서 봤던 기억이 있다.

그 말이 돈 후에는 나랑 몇촌관계인지도 띄워줬던거 같은데 맞나?

하튼 node 간의 평균거리가 '몇촌'에 해당하는걸테고, 평균적으로 7이라고 한다.

실제 그래프가 아닌 랜덤 그래프에서도 작은 세상 효과는 존재한다고 한다. (체인이나 사이클그래프, 격자 그래프는 당근 작은 세상 효과가 존재하지 않는다)

꼬리분포

실제 그래프의 연결성 분포는 두터운 꼬리 분포를 갖는다고 한다. 긴꼬리를 가진다고 보는건데

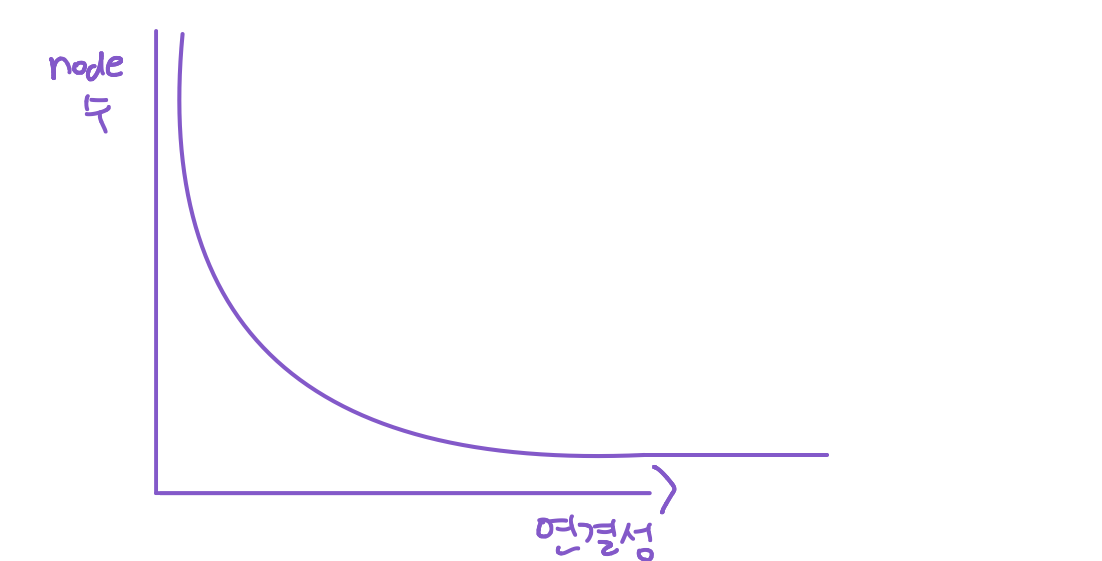
이러한 느김이다. 연결성이 엄청엄청 높은 node의 갯수는 적고, 연결성이 낮은 node의 수가 훨배 많다는거다.

오른쪽으로 갈수록 연예인의 계정, 왼쪽으로 갈수록 일반인의 계정이 되겠다.

연결성이 높은 노드를 hub node라고 한다.

랜덤그래프는 hub가 존재할 확률이 0에 가깝다고 한다.

정규분포처럼 되기 때문이다.

거대 연결 요소

실제 그래프에는 거대 연결 요소(giant connected component)가 존재한다.

거대 연결 요소는 대다수의 정점을 포함한다고 한다.

이번엔 랜덤그래프에서도 존재한다.

단 정점들의 평균 연결성이 1보다 커야하는데

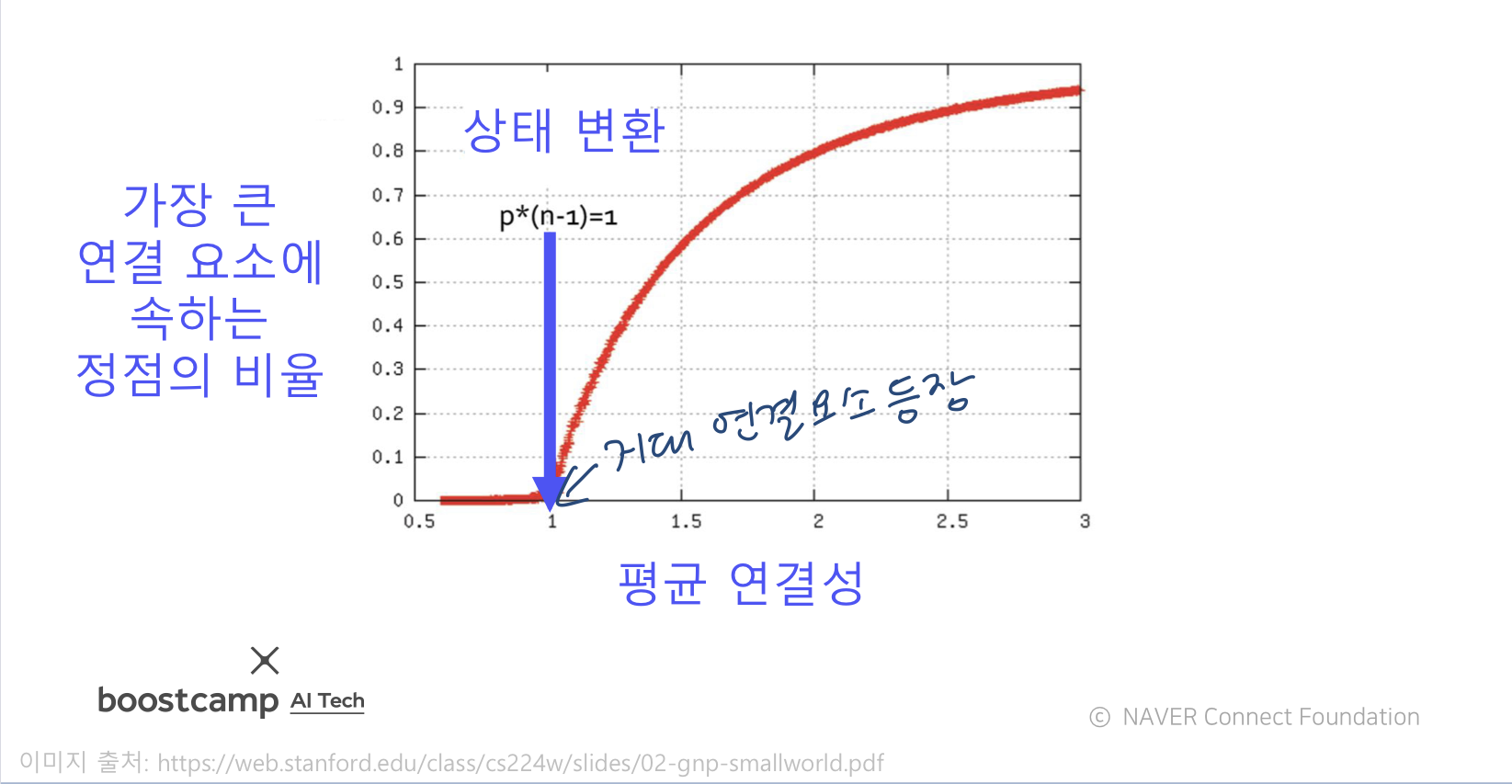
이렇게 1이 되는 순간부터 거대 연결 요소가 등장한다.

군집 계수

군집 계수란 한 정점에서 군집의 형성 정도를 측정한다. 그러니까 node i의 이웃 쌍 중 간선ㅇ로 직접 연결된 것의 비율을 의미하는데,

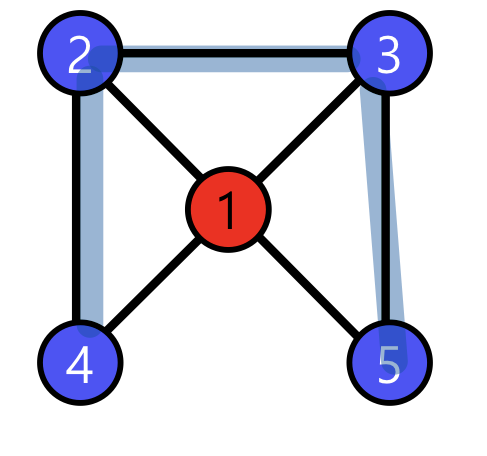
위의 그래프에서 node 1의 군집계수를 구해보자.

1의 이웃 node는 2 3 4 5이다.

이 숫자들의 조합은 (2,3), (2,4), (2,5), (3,4), (3,5), (4,5) 이렇게 여섯개가 나오겠지?

이들 중 실제로 존재하는 선은 (2,3), (2,4), (3,5)이다.

즉 3/6이 노드1의 군집계수이다!

연결성이 0이라면 분모가 0이라 군집계수를 구할 수 없다는 점은 짚고 넘어가자.

이 지역적 군집계수가 높을 수록 높은 확률로 다른 노드들과 연결되어 있는 것이기 때문에 높은 확률로 군집을 형성한다는 걸 알 수 있다.

전역 군집계수는 지역적 군집 계수의 평균이다.

실제 그래프에서는 군집 계수가 높다. 즉 많은 군집이 존재하는데,

동질성(같은 동네 사람들끼리 다 아니까), 전이성(친구 소개로, 건너건너도 알 수 있으니까)

두가지 이유로 실제 그래프에서는 많은 군집이 존재한다.

반면 랜덤 그래프에서는 지역적 혹은 전역 군집 계수가 높지 않다. 간선간의 연결이 독립적이기 때문!

마지막으로 그래프를 쭉 코드로 살펴보며 끝내자.

균일 그래프의 각 노드는 균일한 패턴에 따라서 연결되어있고 일정하게 4개끼리 연결되어있다.

작은 세상 그래프는 균일 그래프의 일부를 임의로 바꿔준거고

랜덤 그래프는 에르되스-레니 그래프를 따른다.

이 친구들을 코드로 나타낼 것이다.